Stabilizacja glikemii pacjentów OIOM przy użyciu regulatora LQ
Artykuł poświęcony jest rozważaniom na temat sposobu automatycznej regulacji poziomu cukru we krwi pacjenta oddziału intensywnej opieki medycznej (OIOM). Opisano w nim model ICU-MM oraz proces projektowania regulatora LQ na podstawie modelu. Omówiono też dwa warianty sterowania systemem (za pomocą insuliny oraz glukozy z insuliną). Na koniec zaprezentowano aplikację wykonaną w języku Python umożliwiająca symulację glikemii pacjenta OIOM.
1. Wstęp
Stan hiperglikemii medycyna defi niuje jako zaburzenie metaboliczne powodujące długotrwałe (ponad dwie godziny od spożycia posiłku) utrzymywanie się poziomu glukozy w osoczu krwi powyżej poziomu 110 mg/dl.
Problem ten, z pozoru charakterystyczny jedynie dla osób cierpiących na cukrzycę, dotyka w sposób szczególny także inną grupę chorych – pacjentów oddziałów intensywnej opieki medycznej (OIOM). W tym przypadku pacjent nie musi być cukrzykiem, by wystąpiła u niego hiperglikemia; wystarczy, że zostanie poddany silnemu działaniu stresu i będzie miało miejsce zaburzenie wewnętrznej homeostazy (zdolność organizmu do zachowania równowagi) organizmu chorego.
Powodem, dla którego hiperglikemia jest zjawiskiem niepożądanym zarówno u osób chorych na cukrzycę, jak i pacjentów przebywających na oddziale OIOM, są jej powikłania. Nawet krótkotrwała hiperglikemia może prowadzić do zwiększenia ryzyka infekcji i czasu gojenia ran, zwiększenia ryzyka bakteriemii i fungemii, zwiększenia prawdopodobieństwa wystąpienia zastoinowej niewydolności serca oraz wstrząsu kardiogennego, chorób stawów, zmian naskórnych, chorób naczyniowych mózgu, śpiączki cukrzycowej, niewydolności nerek.
Interesujące wydaje się stworzenie systemu, który będzie w stanie w krótkim czasie i w bezpieczny sposób, na podstawie aktualnego stanu pacjenta, dobierać dawki insuliny i glukozy w sposób optymalny, a w efekcie przyspieszyć uzyskanie prawidłowej glikemii.
2. Intensive Care Units-Minimal Model (ICU-MM)
Omówimy teraz model służący do opisu dynamiki poziomu cukru we krwi pacjenta, w którym kolejne estymacje glikemii pacjenta są oparte zarówno na insulinie endogennej, jak i insulinie oraz glukozie egzogennej. Cechy te ma zaproponowany w 2007 r. Intensive Care Units-Minimal Model [7].
Model ten jest opisywany za pomocą układu nieliniowych równań różniczkowych:
| (1) | |
| (2) | |
| (3) | |
| (4) |
Jak można zauważyć, poszczególne równania są od siebie zależne. W równaniu (1) wykorzystywana jest wartość zmiennej X(t), której stan określa równanie różniczkowe (2). Równanie to jest zależne od I1(t), którego wartość wyznacza równanie (3) itd. Schemat blokowy systemu przedstawia rys. 1 [4]. Wszystkie parametry opisywane tab. 1 pochodzą z [7].
Ponieważ większość pacjentów w stanie krytycznym nie choruje na cukrzycę, insulina wytwarzana przez trzustkę jest ciągle aktywna i może wspomagać leczenie. Dostarczanie pewnej ilości insuliny za pomocą pompy insulinowej jest wskazane u większości chorych w celu zwiększenia efektywności leczenia. System opisany równaniami (1)–(4) może zatem zostać wykorzystany do konstrukcji systemu automatycznego nadzoru stanu glikemii pacjenta OIOM.
3. Konstrukcja regulatora LQ
W tym miejscu przejdziemy do opisu czynności niezbędnych do konstrukcji regulatora, który pozwoli na szybki jak i bezpieczny sposób regulacji poziomu glikemii we krwi pacjenta.
Do zaprojektowania sterowania systemu (1)–(4) rozwiążemy problem liniowo kwadratowy dla systemu zlinearyzowanego
| (5) |
i wskaźnika jakości
| (6) |
gdzie:
W, R są stałymi macierzami rzeczywistymi,
Jeżeli para (A; B) jest stabilizowalna a para (W; A) wykrywalna, to istnieje sterowanie optymalne minimalizujące wskaźnik jakości (6) o postaci:
| (7) | |
| (8) |
gdzie D=DT>0 jest rozwiązaniem równania różniczkowego:
| (9) |
Dokonamy teraz linearyzacji systemu (1)–(4) i zaprojektujemy regulator dla systemu zlinearyzowanego. System (1)–(4) ma tylko jeden punkt równowagi i jest to [3]:
| (10) |
By przejść do linearyzacji systemu (1)–(4) konieczne jest takie przybliżenie nieróżniczkowalnej funkcji max(0, x), aby możliwe było obliczenie macierzy Jacobiego systemu. Opierając się na pracy [6] będziemy używać następującej aproksymacji
| (11) |
Dzięki przeprowadzonym obliczeniom można wyznaczyć macierz Jacobiego prawej strony układu równań systemu (1)–(4)
| (12) |
Po podstawieniu punktu równowagi do macierzy Jacobiego systemu (1)-(4) uzyskuje się macierz A systemu zlinerayzowanemu
| (13) |
Zbadamy teraz stabilność punktu równowagi systemu, w tym celu musimy wyznaczyć pierwiastki wielomianu charakterystycznego W(λ) = det(λI–A), czyli rozwiązać równanie
| (14) |
Po przekształceniach otrzymujemy
| (15) |
Zgodnie z tab. 1 mamy
| (16) |
Z tego powodu możemy bazować na przybliżeniu (uzasadnia to rys. 3)
| (17) |
Stąd łatwo oszacować części rzeczywiste wartości własnych macierzy A
| (18) |
Na tej podstawie możemy stwierdzić, że punkt równowagi systemu (1)–(4) jest asymptotycznie stabilny w sensie Lapunowa.
Ostatnim etapem przed doborem sterowania dla systemu jest sprawdzenie, czy para (A; B) i (W; A) są odpowiednio stabilizowalna i wykrywalna. Będziemy bazować na twierdzeniach.
Twierdzenie 1. Para macierzy (A; B) jest stabilizowalna wtedy i tylko wtedy, gdy:
gdzie n jest wymiarem macierzy A. (np. [9])
Twierdzenie 2. Para macierzy (W; A) jest wykrywalna wtedy i tylko wtedy, gdy para macierzy (AT; WT) jest stabilizowalna (np. [9]).
Nasz system będzie sterowany za pomocą dwóch typów sterowania:
- sterowanie jedynie insuliną, dla którego macierz sterowania ma postać:
| (19) |
- sterowanie glukozą i insuliną, dla którego macierz sterowania ma postać:
| (20) |
Ponieważ macierz A jest asymptotycznie stabilna więc na mocy twierdzenia 1 pary (A; B1) i (A; B2) są stabilizowalne. Analogicznie para macierzy (W; A) jest wykrywalna dla każdej macierzy W o odpowiednich wymiarach
Sterowanie systemem
Sterowanie insuliną
Dla tego przypadku sterowania macierze wagowe zostały dobrane w następujący sposób:
Otrzymujemy zatem macierz K1postaci:
Widzimy, że sterowanie to nie zmienia trajektorii systemu podstawowego. Zatem możemy uznać, że sterowanie to jest nieskuteczne.
Dzieje się tak ponieważ, macierz S=[λiI–A|B1] dla i = 1, 2, 3, 4 ma pełny rząd, jednak jej minory stopnia 4 mają wartości rzędu 10–15. W konsekwencji mamy do czynienia z sytuacją, gdzie układ jest praktycznie niesterowalny i rząd macierzy S wynika z błędów numerycznych, a nie z właściwości systemu.
Sterowanie glukozą i insuliną
Dla tego przypadku sterowania macierze wagowe zostały dobrane w następujący sposób:
Macierz K2przyjmie postać:
Zastosowane w tym przypadku sterowanie jest bardzo skuteczne. Pożądany poziom cukru dla badanych parametrów osiągnięty został po około 200 minutach. Poza znaczną poprawą zbieżności systemu, należy wspomnieć też o innej korzyści wynikającej z zastosowanego rozwiązania: podawana glukoza pozwoliła zredukować drastyczny spadek poziomu cukru dużo poniżej wartości ustalonej. Minimalna wartość glukozy we krwi zarejestrowana została na poziomie 87,49 mg/dl. Jest to wynikiem znacznie lepszym niż w modelu autonomicznym, gdzie cukier osiągał poziom nawet 63,97 mg/dl.
5. Implementacja symulatora
W celu sprawdzenia omawianych sterowań została opracowana internetowa aplikacja w języku Python [11]. Wykorzystywane są w niej biblioteki NumPy, SciPy, Django, Matplotlib, Python Control System Library oraz JQuery. Program pozwala użytkownikowi na ustawienie podstawowych wartości parametrów opisujących model oraz wyboru typów symulacji, jakie zostaną wykonane. W rezultacie generowane są wykresy wybranych wariantów oraz podsumowania opisujące każdą symulację. Symulacje są wykonywane w środowisku Python. Istnieje również możliwość zapisu przeprowadzonych symulacje do pliku PDF.
6. Podsumowanie
W dobie świata zmagającego się z chorobami cywilizacyjnymi coraz bardziej palącym problemem staje się cukrzyca i związane z nią powikłania. Obecnie u ponad 5 % ogółu populacji występuje zespół problemów metabolizmu cukru. W wielu przypadkach prowadzi on do ciężkich powikłań które mogą się kończyć nawet utratą życia chorych.
Zauważmy również, że nadal nie istnieją efektywne metody leczenia tego stanu, a obecnie znane wymagają od pacjentów i lekarzy stałego monitorowania stanu glikemii [8, 10]. W ten sposób marnowany jest czas i środki, które można przeznaczyć na rozwój medycyny.
Uważamy, że konstrukcja automatycznego systemu dozoru stanu glikemii, nie tylko u pacjenta oddziału OIOM, jest jednym z większych wyzwań jakie stawiane są przed ekspertami w dziedzinie automatyki i teorii sterowania. Nasz projekt pokazuje, w niewielkim zakresie, jak można rozwiązać ten problem. Zdajemy sobie również sprawę, że opracowane przez nas rozwiązania są jedynie wstępem do realizacji pełnie automatycznego systemu kontroli i regulacji glikemii pacjentów oddziałów intensywnej opieki medycznej.
Bibliografia
- Athans M., Falb P.L.: Sterowanie optymalne. Wstęp do teorii i jej zastosowania. WNT, Warszawa 1969.
- Baranowski J.: Modelling of delay in glucose-insulin dynamics. Bio-Algorithms and Med-Systems, 6(12): 123–130, 2010.
- Bauer W., Płuciennik P., Baranowski J., Mitkowski W.: LQ based glucose stabilisation for Intesive Care Unit petients. CMS ’09 Computer Methods and Systems, 26–27 November 2009, Kraków, Poland, Eds. Tadeusiewicz R., Ligęza A., Mitkowski W., Szymkat M., 307–312.
- Bauer W., Płuciennik P.: Symulator glikemii pacjenta oddziału intensywnej opieki medycznej (OIOM). Opiekun pracy: dr inż. Jerzy Baranowski. Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki, Akademia Górnicza-Hutnicza w Krakowie, 2011.
- Chee F., Fernando T.: Closed-Loop Control of Blood Glucose. Springer-Verlag, Berlin Heidelberg, 2007.
- Haverbeke N., Van Herpe T., Diehl M., Van den Berghe G., De Moor B.: Nonlinear model predictive control with moving horizon state and disturbance estimation – application to the normalization of blood glucose in the critically ill. Proceedings of the IFAC World Congress 2008. IFAC World Congress 2008, 9069–9074, Seoul, Korea, 2008.
- Van Herpe T., Espinoza M., Haverbeke N., De Moor B., Van den Berghe G.: Glycemia prediction in critically ill patients using an adaptive modeling approach. Journal of Diabetes Science and Technology, 1(3): 348–356, 2007.
- Janeczko-Sosnowska E.: Nagłe skoki glikemii. hiperglikemia jako kluczowy czynnik ryzyka powikłań cukrzycy. DiabetoLOGIA na co dzień, 2(11): 12–15, 2008.
- Mitkowski W.: Równania macierzowe i ich zastosowania. AGH Uczelniane Wydawnictwa Naukowo-Dydaktyczne, Kraków 2006.
- Zapała E., Strzeszyński Ł., Jaeschke R.: Intensywna insulinoterapia u chorych na internistycznych oddziałach intensywnej terapii. Medycyna Praktyczna, (6), 2006.
- Python Programming Language – Official Website. http://python.org
Waldemar Bauer, Paweł Płuciennik
Słowa kluczowe
blood level ofglucose, glikemia, LQ controller, OIOM, Python, regulator LQR, simulation, symulacja

![Tab. 1. Parametry modelu ICU-MM [Parameters of ICU-MM] Tab. 1. Parametry modelu ICU-MM [Parameters of ICU-MM]](/var/aol/storage/images/par/forum-mlodych/studenckie-kolo-naukowe-integra/stabilizacja-glikemii-pacjentow-oiom-przy-uzyciu-regulatora-lq/66448-2-pol-PL/Stabilizacja-glikemii-pacjentow-OIOM-przy-uzyciu-regulatora-LQ_articleimage.jpg)
![Tab. 1. Parametry modelu ICU-MM [Parameters of ICU-MM] Tab. 1. Parametry modelu ICU-MM [Parameters of ICU-MM]](/var/aol/storage/images/media/par/04_11/fm/tab.jpg/80215-1-pol-PL/tab.jpg_large.jpg)
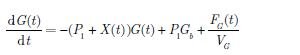
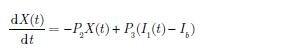
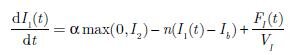
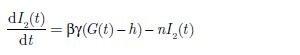
![Rys. 1. Schemat ICU-MM [ICU-MM schema] Rys. 1. Schemat ICU-MM [ICU-MM schema]](/var/aol/storage/images/media/par/04_11/fm/r1.jpg/80230-1-pol-PL/r1.jpg_large.jpg)
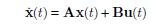
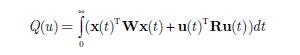

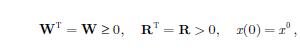
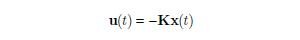
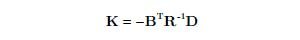
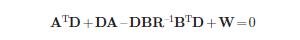
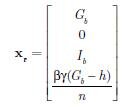
![Rys. 2. Aproksymacja funkcji max(0,I2) [Function max(0,I2) approximation] Rys. 2. Aproksymacja funkcji max(0,I2) [Function max(0,I2) approximation]](/var/aol/storage/images/media/par/04_11/fm/r2.jpg/80257-1-pol-PL/r2.jpg_large.jpg)
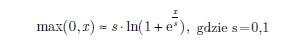
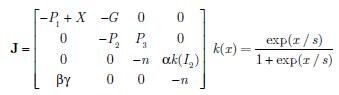
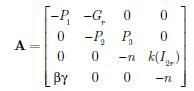
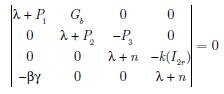
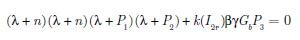
![Rys. 3. a) Przybliżony wykres funkcji (17), b) Przybliżony wykres funkcji (15) [a) Approximate plot of function (17), b) Approximate plot of function (15)] Rys. 3. a) Przybliżony wykres funkcji (17), b) Przybliżony wykres funkcji (15) [a) Approximate plot of function (17), b) Approximate plot of function (15)]](/var/aol/storage/images/media/par/04_11/fm/r3.jpg/80275-1-pol-PL/r3.jpg_large.jpg)
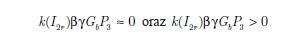
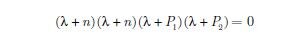
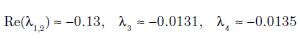
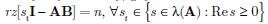
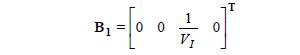
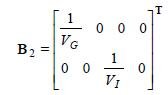
![Rys. 4. Sterowanie insulinowe [Control of insulin] Rys. 4. Sterowanie insulinowe [Control of insulin]](/var/aol/storage/images/media/par/04_11/fm/r4.jpg/80296-1-pol-PL/r4.jpg_large.jpg)

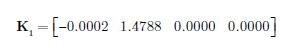
![Rys. 5. Sterowanie glukozowo-insulinowe [Control of glucose-insulin] Rys. 5. Sterowanie glukozowo-insulinowe [Control of glucose-insulin]](/var/aol/storage/images/media/par/04_11/fm/r5.jpg/80305-1-pol-PL/r5.jpg_large.jpg)
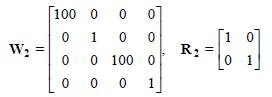
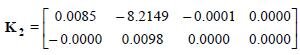
![Rys. 6. Symulator glikemii [Simulator of blood level of glucose] Rys. 6. Symulator glikemii [Simulator of blood level of glucose]](/var/aol/storage/images/media/par/04_11/fm/r6.jpg/80314-1-pol-PL/r6.jpg_large.jpg)