System automatycznych pomiarów rynometrycznych (3)

 

Przegląd metod

W związku z upowszechnieniem się skanerów powierzchni i obrazów przestrzennych, w ostatnich latach nastąpiło znaczne natężenie prac w obszarze ich analizy. Bardzo intensywne prace prowadzi się w zakresie badania obrazów powierzchni twarzy, co wiąże się z nadziejami na zastosowanie ich do weryfikacji tożsamości. Wyróżnia się podejścia:

• holistyczne – polegające na całościowym porównaniu współrzędnych punktów sceny z pewnymi wzorcami, bez próby odzyskania pośredniej, użytecznej dla człowieka, informacji o charakterystyce danych;
• oparte na ekstrakcji cech, w którym najpierw pozyskiwana jest informacja o cechach (wybranych punktach, charakterystykach) danych; dopiero odzyskana informacja o cechach poddawana jest dalszej analizie.

Zgodnie z postawionym celem, tj. pozyskaniem informacji o charakterystykach wybranego regionu twarzy (nosa), interesująca jest wyłącznie druga grupa metod. W jej obszarze główne kierunki prowadzonych prac przypisać można do jednej z klas [1]:

• metody oparte na geometrii różniczkowej (curvature analysis-based) – techniki oparte na analizie matematycznej kształtu, które biorą swój początek z prób opisu i charakteryzowania obiektów dowolnego kształtu (free-form objects) podejmowanych od połowy lat 80-tych; metody te są najszerzej znane i najbardziej rozpowszechnione;
• metody specjalizowane dla cech – grupa technik opartych na próbie odzyskiwania informacji o poszczególnych cechach; korzystają one ze specyfiki danej cechy np. poszukiwanie czoła jako największego płaskiego obszaru twarzy;
• metody oparte na deskryptorach punktów (shape representation-based methods) – techniki, w których dla każdego punktu sceny buduje się pewien zestaw danych charakterystycznych, a następnie próbuje dopasować punkty wzorca (obrazu wzorcowego) i obrazu testowanego (chmura punktów do przeanalizowania).

Deskryptory punktów

Deskryptory punktów należą do metod statystycznych i to czyni je dobrym narzędziem do analizy danych mogących zawierać błędy i przekłamania. Koncepcyjnie są rozwiązaniem dość prostym, ale kolejne ich zastosowania i wariacje pokazują duży potencjał w użyciu do analizy obiektów dowolnego kształtu. Jako rozwiązanie stosunkowo młode, deskryptory są wciąż atrakcyjne z punktu widzenia badań. Ich złożoność obliczeniowa waha się, w zależności od sposobu użycia, co pozwala na dalsze dociekania w zakresie optymalizacji.

W podejściach opartych na deskryptorach, ze zbioru punktów analizowanego obrazu (sceny), wybierany jest podzbiór punktów. Następnie dla każdego z nich w podzbiorze obliczany jest deskryptor – struktura go charakteryzująca. Budując deskryptory zwykle korzysta się z położeń względnych (np. względem punktu, dla którego obliczany jest histogram), co czyni je niewrażliwymi na przesunięcia. Zwykle są też odporne na obroty. Istnieje kilka typów deskryptorów, z których najpopularniejsze to:

• spin image (obraz obrotu)
• local surface patch („łatka’’ lokalnej powierzchni)
• shape context (kontekst kształtu)
• local shape map (mapa lokalnego kształtu)
• point signature (sygnatura punktu).

Dalej przybliżono pierwsze cztery. Łączy je to, że każdy z nich do liczbowego scharakteryzowania punktu stosuje dwuwymiarowy histogram.

Local surface patch

Ciekawą strukturą opisującą punkt wraz z jego otoczeniem jest LSP (Local Surface Patch). LSP opisuje wycinek obiektu o promieniu r wokół punktu p. Na deskryptor punktu składają się:

• typ powierzchni określony przez indeks kształtu (shape index)
• centroid wycinka (zauważyć należy, że niekoniecznie jest on równy punktowi p)
• dwuwymiarowy histogram
• indeks kształtu – miara wprowadzona w geometrii różniczkowej, która mapuje lokalne kształty powierzchni w wartości z przedziału [0, 1] i opisuje kształt powierzchni niezależnie od ułożenia w przestrzeni. Dokładniej scharakteryzowana zostanie w kolejnych częściach artykułu.

W LSP sąsiedzi (ozn. q) punktu p zdefiniowani zostali jako punkty, których położenie zawiera się w pewnej sferze o środku w p i promieniu r: ||q – p|| r. Dodatkowym kryterium jest, aby kierunek normalnej do powierzchni w punkcie sąsiednim q zbliżony był do kierunku normalnej w punkcie p: a·cos(n_p, n_q) A, gdzie:

• n_p – wektor normalny do powierzchni w punkcie p
• n_q – wektor normalny w punkcie q będącym potencjalnym sąsiadem
• A – stała określająca próg.

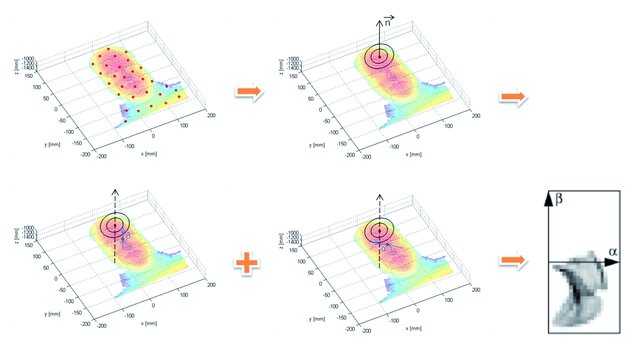
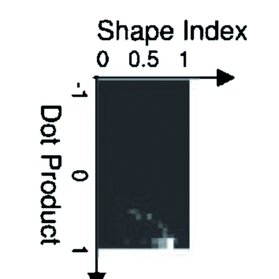
Kluczowym elementem LSP jest histogram określający rozkład cech sąsiadów punktu p. Na jednej z osi histogramu odkładane są wartości indeksu kształtu. Druga określa wartości iloczynu skalarnego (dot product) między kierunkami normalnymi do powierzchni w punkcie p i w punktach sąsiednich: n_p · n_q. W celu redukcji szumu stosowana jest interpolacja dwuliniowa (bilinear interpolation). Przykład LSP pokazano na rys. 1.

Shape context feature

Shape context features wprowadzone zostały [2] celem rozpoznawania obiektów dwuwymiarowych, w szczególności liter pisma odręcznego. W shape context features dla każdego punktu definiowany jest deskryptor: dwuwymiarowy histogram (shape context) liczby punktów. Z każdym punktem p, dla którego budowany jest deskryptor, wiąże się biegunowy układ współrzędnych. Jego początek znajduje się w tym punkcie. Oś biegunowa może mieć kierunek stały dla wszystkich deskryptorów, lub też być położona pod kątem prostym do kierunku krawędzi obiektu. To drugie podejście czyni metodę odporną na obroty. W nowym układzie współrzędnych każdemu punktowi obiektu odpowiada para współrzędnych:

• r_p – odległość od punktu p: r_p = ||p - q||
• Θ – kąt względem osi biegunowej.

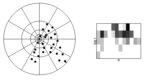
Stosując nowy układ współrzędnych, buduje się dwuwymiarowy histogram położenia punktów (rys. 2). Na jednej osi odkładany jest log(r_p). Druga odpowiada wartościom kąta Θ.

Spin image i Local shape map

Reprezentacją danych 3D odporną na obroty i przesunięcia są obrazy obrotu (spin images). Również one wykorzystują dwuwymiarowe histogramy.

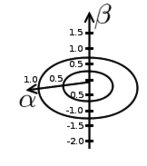
W punkcie p, dla którego budowany jest deskryptor, umiejscawiany jest zmodyfikowany walcowy układ współrzędnych (rys. 3). Kierunek jednej z osi jest zdeterminowany przez kierunek wektora normalnego do powierzchni w tym punkcie: n_p. Pozostałe dwie osie nie są ściśle określone. Znana za to jest płaszczyzna je zawierająca – jest wyznaczona jako płaszczyzna styczna (tangent) do powierzchni obiektu w punkcie ozn. Tan_p. Tak zbudowany układ (oś i płaszczyzna) pozwala przyporządkować każdemu z punktów obiektu dwie współrzędne:

• α – odległość radialna; odległość do osi określonej przez kierunek wektora normalnego w punkcie p, co symbolicznie można zapisać: α = |q - n_p|
• ß – odległość (wraz ze znakiem determinującym położenie nad/pod) do płaszczyzny stycznej do powierzchni w punkcie: ß = sign(q - Tan_p) · |q - Tan_p|.

Przy budowie histogramu (spin image) przestrzeń dzieli się na ”kubełki” odpowiadające kolejnym przedziałom wartości α i β. Następnie zliczana jest liczba punktów obiektu trafiających do danego ”kubełka”. W zależności od przyjętej liczby przedziałów uzyskuje się deskryptory (histogramy) o różnej rozdzielczości. Procedurę ilustrują rys. 4 i 5.

Deskryptorem koncepcyjnie bardzo podobnym do spin image jest LSM (Local Shape Map). Różni je od siebie sposób definiowania współrzędnej α. W LSM obliczana jest ona jako odległość punktu od środka układu współrzędnych α = ||q - p|| (umiejscowionego w punkcie, dla którego obliczany jest deskryptor). Dodatkowo przy budowie histogramu LSM uwzględniane są jedynie punkty położone w pewnej ograniczonej odległości r od punktu, dla którego budowany jest deskryptor: ||q - p|| r.

Podsumowanie

W artykule dokonano krótkiej klasyfikacji metod analizy obiektów 3D dowolnego kształtu. Omówiono i wprowadzono deskryptory punktów, jako ważne narzędzia służące opisowi charakterystyk lokalnych sceny. W kolejnej części temat deskryptorów będzie rozwijany. Rozważone zostaną kluczowe aspekty ich stosowania: wybór sąsiedztwa, typ osi histogramów. Wprowadzone zostanie pojęcie odległości między deskryptorami. Przeanalizowane zostaną różne strategie wyboru punktów, dla których budowane są deskryptory.

Bibliografia

1. Zhnohui Wu, Yueming Wang, Gang Pan, editors: 3D Face Recognition Using Local Shape Map. Department of Computer Science and Engineering Zhejiang University, Hangzhou, IEEE, 2004. 2004 International Conference on Image Processing (ICIP).
2. Belongie S., Malik J., Puzicha J.: Shape matching and object recognition using shape contexts. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24(24), April 2002.
3. Johnson A.E., Hebert M.: Using spin images for efficient object recognition in cluttered 3d scenes. IEEE Transactions on Pattern Analysis and Machine Intelligence, 21(5), May 1999.
4. Hui Chen, Bir Bhanu: 3d free-form object recognition in range images using local surface patches. Pattern Recognition Letters, 28:1252–1262, 2007.
5. Chin Seng Chua, Feng Han, Yeong-Khing Ho, editors: 3D Human Face Recognition Using Point Signature. School of Electrical and Electronic Engineering, Nanyang Technological University, IEEE, 2000. 4th IEEE International Conference on Automatic Face and Gesture Recognition (FG’00).
6. Chin Seng Chua, Jarvis R.: Point signatures: A new representation for 3d object recognition. International Journal of Computer Vision, 25(1): 63–85, 1997.
7. Yang Li, Smith W.A.P., Hancock E.R., editors: Face Recognition using Patch-based Spin Images. Department of Computer Science, University of York, IEEE, 2006. 18th International Conference on Pattern Recognition (ICPR’06).

Tomasz Kuśmierczyk – Studenckie Koło Naukowe Cybernetyki, Politechnika Warszawska