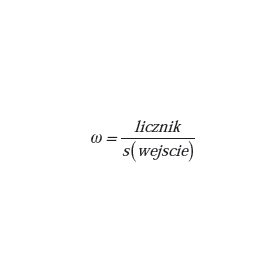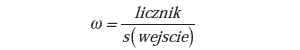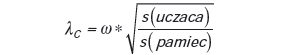Badania porównawcze klasyfikatora BARBARA na zbiorze parametrów medycznych osób z chorobą Parkinsona

 

Lekarza można jednak zastąpić aparaturą zbierającą próbki mowy, a następnie klasyfikującą je. Wśród wielu metod klasyfikacji do najpopularniejszych zalicza się: metodę K-NN [7, 8], sieci neuronowe [7, 6] oraz systemy immunologiczne [3, 4, 5]. Użycie odpowiedniego algorytmu zależy zwykle od charakteru danych, dlatego wybór klasyfikatora musi być poprzedzony staranną analizą problemu klasyfikacji.

W artykule prezentowany jest nowy algorytm klasyfikacyjny, który może śmiało konkurować z rozwiązaniami dostępnymi na rynku. Przedstawione są również testy porównawcze klasyfikatora BARBARA [3] oraz innych popularnych metod.

Przyjęte miary klasyfikacji

Najprostszą miarą sprawdzenia jakości klasyfikacji jest porównanie klasy danych wejściowych z danymi wyjściowymi. Przykładowo, na wejściu podajemy wektor danych, który mamy zamiar sklasyfikować, dodatkowo jako drugi parametr podajemy numer klasy tego wektora. Na wyjściu procedury testowej klasyfikacji powinien być wynik stwierdzający czy klasa wektora wejściowego jest taka sama jak klasa wyjściowa. Jeśli tak, to można inkrementować licznik poprawnie sklasyfikowanych wektorów. Stopień klasyfikacji oblicza się ze stosunku poprawnie sklasyfikowanych danych i liczby wszystkich wektorów w macierzy wejściowej (1)

(1)

gdzie: licznik – licznik poprawnie sklasyfikowanych wektorów, podanych na wejściu klasyfikatora, wejscie – macierz wektorów wejściowych, s – funkcja wielkości.

Taka miara może nie być miarodajna dlatego, że nie określa, w jakim stopniu klasyfikator zgeneralizował dane wejściowe. Powszechnie wiadomo, że przetwarzanie danych testowych przez klasyfikator służy zgeneralizowaniu danych (skompresowaniu), dzięki czemu dalsze operacje przeszukujące, będą mogły działać na mniejszym zbiorze danych, a jakościowo tożsamym lub bardzo zbliżonym do zbioru wejściowego.

Wniosek: Idealnym klasyfikatorem nazywać będziemy taki algorytm, który będzie maksymalizował stopień klasyfikacji ω (1) i jednocześnie minimalizował wielkość zbioru wejściowego.

Zaproponowano zatem współczynnik doskonałości klasyfikacyjnej λ_c

(2)

gdzie: uczaca – macierz wejściowa podawana klasyfikatorowi do generalizacji, pamiec – macierz wyjściowa algorytmu klasyfikacji, zgeneralizowana i skompresowana macierz ucząca (pozbawiona redundantności), s – funkcja wielkości, ω – współczynnik opisany wzorem (1).

Miara ta umożliwia jednoczesne zmierzenie jakości klasyfikacji i wielkości zbioru wynikowego, dzięki czemu realne jest dobranie optymalnego klasyfikatora dla danego problemu.

Klasyfikator BARBARA

Klasyfikator BARBARA miał na celu poprawienie klasyfikacji i grupowania danych algorytmu K-NN [3] w porównaniu z sieciami neuronowymi [7]. Klasyfikator BARBARA jest zmodyfikowaną wersją algorytmu K-NN, która potrafi sama rozpoznawać klasy. Zaproponowany klasyfikator w porównaniu z algorytmem K-NN jest na tyle elastyczny, że można go wykorzystać w analizie wysokoprzepustowych danych [3].

Algorytm klasyfikatora BARBARA Normalizuj parametrami macierz Mwejściowa do zakresu [0, 1] dla każdej zmiennej Mwejściowai gdzie i = 1, ..., n wykonaj Znajdź wszystkie podobne wektory pod względem funkcji korelacja Zapisz znalezione wektory do macierzy tymczasowej X Posortuj wektory pod względem największej wartości funkcji korelacja Utwórz tymczasową macierz X’ zamierającą k najlepiej dopasowanych wektorów, jednocześnie wykonaj Mwejściowa = Mwejściowa X’ Jeżeli wykonywana jest klasyfikacja, to znajdź dominującą klasę wśród wektorów macierzy X’ i zachowaj ją w zmiennej klasa. Dokonaj uśredniania parametrów (kolumn) macierzy X’: jeżeli parametr jest zmienną jakościową, to znajdź dominującą wartość parametru (dominantę), w przeciwnym wypadku parametr jest zmienną ilościową i należy go uśrednić za pomocą średniej arytmetycznej Dodaj powstały wektor do macierzy wyjściowej M i jeśli wykonywaną operacją była klasyfikacja, to przypisz mu klasę zapisaną w zmiennej klasa.

Zastosowane w algorytmie oznaczenia:

Mwejściowa – macierz poddawana klasyfikacji bądź grupowaniu
korelacja – funkcja badająca korelację (korelacja Pearsona, korelacja R² lub inna)
X, X’ – tymczasowe macierze, w których zapisywane są podobne wektory
k – zmienna zawierająca liczbę wektorów przechodzących do następnego poziomu algorytmu
klasa – zmienna pomocnicza, w której zapisywana jest dominująca klasa w macierzy
M – macierz wyjściowa.

Generalnie algorytm bazuje na zasadzie dostosowywania się do większości. Na początku realizowane jest wyszukiwanie najbardziej podobnych wektorów pod względem korelacji (grupowanie [8]), a następnie wykonywane jest dostosowanie. Dostosowanie polega na uśrednieniu parametru ilościowego średnią arytmetyczną, a parametru jakościowego, dominantą. Otrzymany w ten sposób wektor zawiera najważniejsze cechy wszystkich k wektorów składowych. Wektorowi temu przypisywana jest klasa dominująca w macierzy X'.

Algorytm BARBARA można nazwać algorytmem dostosowanych k-najbardziej podobnych wektorów.

Tab. 1. Opis najważniejszych atrybutów

Atrybut	Opis	Opis po angielsku
name	nazwa symboliczna osobnika, od którego pobierano próbkę głosu	symbolic name of the individual from whom the sample collected voice
MDVP:Po(Hz)	średnia częstotliwość podstawowa głosu	average vocal fundamental frequency
MDVP:Fhi(Hz)	maksymalna częstotliwość podstawowa głosu	maximum vocal fundamental frequency
MDVP:Flo(Hz)	minimalna częstotliwość podstawowa głosu	minimum vocal fundamental frequency
MDVP:Jitter(%), MDVP:Jitter(Abs) MDVP:RAP MDVP:PPQ Jitter:DDP	miary zmian częstotliwości bazowej	several measures of variation in fundamental frequency
MDVP:Shimmer, MDVP:Shimmer(dB) Shimmer:APQ3 Shimmer:APQ5 MDVP:APQ Shimmer:DDA	miary zmian amplitudy bazowej	several measures of variation in amplitude
NHR HNR	środki wskaźnika hałasu, na składniki tonowe w głosie	two measures of ratio of noise to tonal components in the voice
status	stan zdrowia osobnika (jeden) - chory, (zero) - zdrowy	health status of the subject (one) - Parkinson's, (zero) - healthy
RPDE D2	nieliniowa dynamiczna złożoność działań	two nonlinear dynamical complexity measures
spread1 spread2 PPE	nieliniowe środki podstawowych zmian częstotliwości	three nonlinear measures of fundamental frequency variation
DFA	wykładnik skalowania sygnału fraktalnego	signal fractal scaling exponent

Badania przeprowadzone na zbiorze danych

Zbiór danych pacjentów z chorobą Parkinsona

Analizowane dane są udostępnione przez UCI Repository University of California [1]. Zbiór ten stworzył Max Little z University of Oxford w Anglii we współpracy z National Centre for Voice and Speech w Denver, Colorado [2]. Przeprowadzono badania wymowy 31 osobników, z których 21 miało chorobę Parkinsona, a 10 jej nie miało. Od wszystkich osobników pobrano średnio 6 próbek głosu, co w sumie dało 195 wektorów opisujących głosy wszystkich osobników. Każdy wektor ma 23 atrybuty (tab. 1).

Wszystkie atrybuty mają za zadanie pomóc w poprawnym sklasyfikowaniu choroby Parkinsona. Zmienną celu jest atrybut status, który opisuje czy dany osobnik jest chory na chorobę Parkinsona - wartość 1, czy jest zdrowy - wartość 0.

Wstępne przetworzenie danych

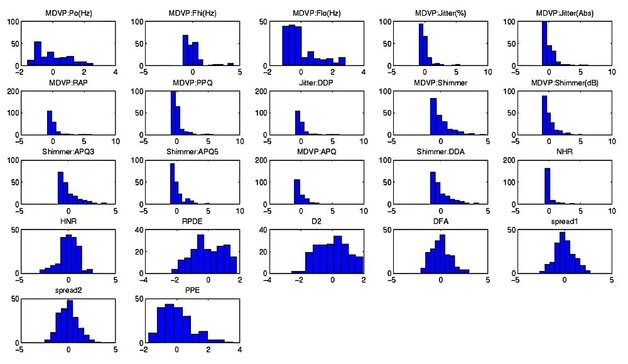
Wyniki pomiarów medycznych [1] zostały ustandaryzowane. Usunięto parametr name określający osobnika, a parametr status przekształcono na zmienną celu. Do badań pozostały 22 atrybuty, których histogramy przedstawia rys. 1. Ich analiza pozwala zauważyć, że histogramy większości parametrów mają kształt rozkładu zbocza opadającego (np. MDVP, Shimmer, NHR). Histogramy niektórych parametrów mają z kolei rozkład normalny (np. spread1, spread2, DFA). Informacje zawarte na histogramie mogą być pomocne przy analizie parametrów [8].

Dane zostały podzielone w sposób losowy na dwa zbiory: zbiór uczący – 97 wektorów oraz zbiór testowy – 98 wektorów.

Badania algorytmów klasyfikacji

Tab. 2. Klasyfikacja surowych danych

Klasyfikator	ω	λc
Surowe dane	0,96938	0,96938

W pierwszej fazie przetestowano stopień dopasowania tzw. surowych danych (nieprzetworzonych żadnym klasyfikatorem danych uczących). Wynik klasyfikacji przedstawiono w tab. 2.

Jak widać, ω = λ_c. Równość ta występuje tylko w przypadku, gdy nie dokonano generalizacji danych wejściowych.

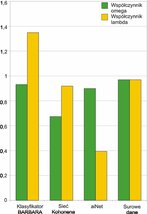
Oprócz testu na surowych danych wykonano testy klasyfikacji algorytmów BARBARA, sieci Kohonena [3, 6] oraz systemu immunologicznego aiNet [3, 4, 5]. Wyniki testów zebrano w tab. 3 oraz na rys. 2 przedstawiającym wykres współczynnika doskonałości klasyfikacyjnej λ_c oraz ω.

Tab. 3. Wyniki testów klasyfikacji poszczególnych algorytmów

Algorytm	ω	λc	max (ω)	max (λc)
Klasyfikator BARBARA	0,931252	1,348982	0,969400	1,378716
Sieć Kohonena	0,562937	0,768857	0,673071	0,919282
aiNet	0,898673	0,393218	0,928600	0,462502
Surowe dane	0,969388	0,969388	0,969388	0,969388

Współczynnik klasyfikacji ω przyjmuje najwyższą wartość przy testowaniu danych niezgeneralizowanych i wynosi ω»0,97. Gorsze wyniki klasyfikacji dały kolejno: algorytm BARBARA (ω»0,93), aiNet (ω»0,90), sieć Kohonena (ω»0,56). Ranking pod względem współczynnika λ_c wygląda trochę inaczej. Wynika to z tego, że współczynnik λ_c uwzględnia również stopień kompresji danych uczących (2). Najlepszy wynik dla współczynnika λ_c osiąga klasyfikator BARBARA (λ_c»1,35), gorszy wynik dała metoda testowania surowych danych (λ_c»0,97), sieć Kohonena (λ_c»0,77) oraz system immunologiczny aiNet (λ_c»0,39).

Podsumowanie

Przeprowadzone badania i ocena wyników wskazują, że najlepszy średni wynik klasyfikacji pod względem współczynnika λ_c miał klasyfikator BARBARA, drugim po nim była metoda testowania surowych danych, kolejnym algorytmem była sieć Kohonena (rys. 2). Klasyfikator bazujący na zasadzie sztucznego systemu immunologicznego – aiNet dał najgorszy wynik współczynnika doskonałości λ_c dla danych testowych.

Analizując wyniki klasyfikacji pod kątem współczynnika w, najlepiej wypadł test surowych danych, zaraz za nim był klasyfikator BARBARA, następnie sieć Kohonena. Najgorsze wyniki dał klasyfikator aiNet. Wyniki przedstawione na wykresie potwierdza tab. 3.

Reasumując, aby minimalizować wyjściową macierz pomiarów procesem klasyfikacji przy jednoczesnym zachowaniu 90 % wiedzy zbioru uczącego dla pomiarów parametrów medycznych, należy użyć klasyfikatora BARBARA. System immunologiczny zwraca niewiele mniejszą wartość testu klasyfikacji, ale jednocześnie zwiększa objętość macierzy wyjściowej. Najgorsze wyniki klasyfikacji przedstawionych danych pacjentów zwróciła sieć Kohonena.

Klasyfikator BARBARA wydaje się być dobrym wyborem w systemach wbudowanych oraz w systemach przetwarzających duże ilości danych. Dzięki prostej budowie, a zarazem skuteczności przy dużych zbiorach pomiarowych, klasyfikator ten może być atrakcyjnym rozwiązaniem dla takich dziedzin, jak automatyka, robotyka, systemy sterowania, przetwarzanie obrazów, data mining oraz wielu innych.

Bibliografia

1. UC Irvine Machine Learning Repository.
2. Little M.A., McSharry P.E., Roberts S.J., Costello D.A.E., Moroz I.M.: Exploiting Nonlinear Recurrence and Fractal Scaling Properties for Voice Disorder Detection. BioMedical Engineering OnLine 2007.
3. Myśliwiec K. S.: Przegląd metod sztucznej inteligencji w ekstrakcji danych. Praca inżynierska, PWSZ Krosno, 2010.
4. Castro L.N., Zuben F. J.: Artifical Immune System. Part I – Basic Theory and Applications. Technical Report, 1999.
5. Wierzchoń T.: Sztuczne Systemy Immunologiczne. Akademicka Oficyna Wydawnicza EXIT, 2001.
6. VesantoJ., Himberg J., Alhoniemi E., Parhankangas J.: SOM Toolbox for MATLAB 5. Technical Report A57, Helsinki University of Technology, 2000.
7. Grabska-Chrząstowska J., Libuszowski W., Tomalak W.: Porównanie metody KNN i techniki sieci neuronowych w klasyfikacji badań spirometrycznych. Bio-Algorithms and Med-Systems, Journal edited by Medical College – Jagiellonian University, 2005, Vol. 1, No. 1/2, p. 9–12.
8. Larose D.T.: Metody i modele eksploracji danych. Wydawnictwo Naukowe PWN, 2008.

inż. Kamil Sławomir Myśliwiec – Państwowa Wyższa Szkoła Zawodowa w Krośnie

Ukończył Państwową Wyższą Szkołę Zawodową w Krośnie na kierunku informatyka, o specjalności Sieciowe Systemy Informatyczne. Obronił tytuł inżyniera z oceną 5.0 (bdb). Interesuje się bioinformatyką oraz jej zastosowaniami w takich dziedzinach jak klasyfikacja, predykcja, estymacja danych, jak również zastosowaniem nowych algorytmów sztucznej inteligencji w hurtowniach danych. Oprócz zainteresowań związanych z bioinformatyką, ciekawią go takie dziedziny, jak inżynieria programowania, Web-Service oraz programowanie systemowe.